Pretrained Transformer Language Models for Search - part 3

Photo by Frank Busch on Unsplash
Updated 2022-10-21: Added links and clarified some sections
In this blog series we demonstrate how to represent transformer models in a multiphase retrieval and ranking pipeline using Vespa.ai. We also evaluate these models on the largest Information Retrieval relevance dataset, namely the MS Marco Passage ranking dataset. We demonstrate how to achieve close to state-of-the-art ranking using miniature transformer models with just 22M parameters, beating large ensemble models with billions of parameters.
- Post one: Introduction to neural ranking and the MS Marco passage ranking dataset
- Post two: Efficient retrievers, sparse, dense, and hybrid retrievers
- Post three: Re-ranking using multi-representation models (ColBERT)
- Post four: Re-ranking using cross-encoders)
In the first post in this series we introduced using pre-trained language models for ranking and three popular methods for using them for text ranking. In the second post we studied efficient retrievers that could be used as the first phase in a multiphase retrieval and ranking pipeline. In this third post we study a re-ranking model which we will deploy as a re-ranker on top of the retriever methods we studied in the previous post, but first let us recap what a multiphase retrieval and ranking pipeline is. In a multiphased retrieval and ranking pipeline, the first phase retrieves candidate documents using a cost-efficient retrieval method and the more computationally complex cross-attention or late interaction model inference is limited to the top ranking documents from the first phase. In this post we will study the Contextualized late interaction over BERT (ColBERT) model and deploy it as a re-ranking phase on top of the dense retriever that we studied in the previous post. The CoLBERT ranking model was introduced in ColBERT: Efficient and Effective Passage Search via Contextualized Late Interaction over BERT by Omar Khattab and Matei Zaharia.
Contextualized late interaction over BERT (ColBERT)
In the previous post in this series we introduced a dense retriever using a bi-encoder architecture over a Transformer model (MiniLM). Both queries and documents were encoded by the bi-encoder and represented in the same dense embedding vector space. We used cosine similarity between the query and the document in this embedding vector space to rank documents for a query, and we could accelerate the retrieval phase using approximate nearest neighbor search using angular distance or innerproduct.
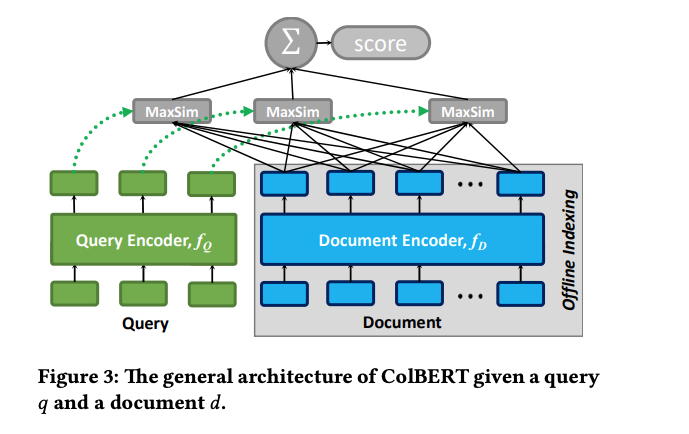
Unlike the dense bi-encoder, the contextualized late interaction model represents the query and document as multiple vectors obtained from the last output layer of the Transformer model. Bi-encoders on the other hand, usually performs a pooling operation over the last transformer layer, e.g. just using the embedding representation from the CLS output token, or mean over all token output embeddings. Also, unlike other text to vector representations like Word2Vec, the token vector representation depends on the other tokens in the same input sequence. For example the token driver in the text Microsoft driver has a different vector representation than driver in the text Taxi driver as the context is different. This thanks to the attention mechanism in the Transformer architecture where each token attends to all other tokens in the same input sequence. We can say that token output vector representation is contextualized by the other tokens in the input text sequence.
Similar to the single vector bi-encoder model, queries and documents are encoded independently. Hence, the query tokens only attend to other query tokens, and document tokens only attend to other document tokens. This separation enables offline processing of the documents which speeds up re-ranking as at re-reranking time we only need to obtain the query token embeddings and load the precomputed document embeddings from storage (e.g. memory). The ColBERT architecture also uses a query encoder and a document encoder, based on the same Transformer instance. The input to the model is different for queries and documents. The query encoder pads using the BERT mask token to a configurable maximum query length if the query input text is shorter than this max length. The document input is not padded to a fixed length. The padding of masked tokens of the query input is explained in the paper:
We denote the padding with masked tokens as query augmentation, a step that allows BERT to produce query-based embeddings at the positions corresponding to these masks. Query augmentation is intended to serve as a soft, differentiable mechanism for learning to expand queries with new terms or to re-weigh existing terms based on their importance for matching the query
The dimensionality used to represent the output token embedding can be reduced using a dimension reduction layer on top of the last output transformer layer. The original token output dimensionality depends on the Transformer model used, for example, the bert-base model uses 768 dimensions while MiniLM uses 384 dimensions. In the ColBERT paper the authors uses dimension reduction to 128 dimensions from the original hidden size of 768 dimensions. The authors also demonstrate that reducing the dimensionality further to 32 does not impact ranking accuracy significantly. The dimensionality used and the precision used for the vector values matters for both the computational complexity and storage requirements. For example, if we use 32 dimensions with bfloat16 (2 bytes per tensor value) precision, we need to store 32GB of vector data for 9M documents with average 60 tokens per document. While if we use 128 dimensions with float32 (4 bytes) precision, we end up with about 256GB of vector data.
Ranking with ColBERT - Meet MaxSim
So we now know roughly how the ColBERT architecture works; Query text is encoded into a fixed length bag of token embeddings and document text is encoded into a bag of token embeddings. But the missing piece is how do we compute the relevancy score of a query, document pair using this representation?
The ColBERT paper introduces the late interaction similarity function which they name Maximum Similarity (MaxSim): For a given query and document pair the MaxSim relevancy score is calculated as follows:
For each query token embedding perform cosine similarity against all the document token embeddings and track the maximum score per query token.
The overall query, document score is the sum of these maximum cosine scores.
For a query with 32 token embeddings (max query length 32), and a document with 128 tokens we need to perform 32*128 cosine similarity operations. The MaxSim operator is illustrated in the figure below.
MaxSim illustration from the ColBERT paper
The cosine similarity with unit length vectors can be performed by the inner dot product, and can be HW accelerated using advanced vector instructions.
Vespa ColBERT representation
To represent the ColBERT model architecture in Vespa for re-ranking documents we need:
- Store the document token embeddings in our Vespa document model for fast, on-demand, access in ranking phases
- Express the MaxSim function with a Vespa ranking expression
- Map the query text to token ids, and map tokens to token embeddings at run time by invoking the ColBERT query encoder transformer model
We expand the Vespa document schema from the previous post and introduce a new mixed Vespa tensor field called dt. We use this tensor to store the computed bag of token embeddings for the document. The mixed tensor (combining sparse dt, and indexed x dimensions) allows storing a dynamic number of token embeddings for the document, depending on the length of the document. We could have used an indexed representation, but that would have used more memory as we would need to determine a max document length.
Vespa Passage document schema
The new document schema including the new dt ColBERT document tensor is given below:
search passage {
document passage {
field id type int {...}
field text type string {...}
field mini_document_embedding type tensor<float>(d0[384]){...}
field dt type tensor<bfloat16>(dt{}, x[32]){
indexing: attribute
attribute:fast-search
}
}
}
The tensor cell value precision type we use is bfloat16 which is 2 bytes per tensor cell value which saves 50% of the memory compared to float precision (4 bytes per value). Vespa supports double, float, bfloat16 and int8 tensor cell value precision types.
We also use 32 dimensions for the per token embedding representation instead of 128 to further reduce the memory requirement. The indexing statement specifies attribute which means this field will be stored in-memory and fast-search enables fast uncompressed representation in memory which speeds up evaluation over mixed tensor fields. fast-search is only relevant for mixed tensor type fields.
Vespa MaxSim operator
We can express the MaxSim operator in Vespa by a tensor ranking expression using sum and reduce tensor functions.
sum(
reduce(
sum(query(qt) * attribute(dt), x),
max, dt
),
qt
)
Where attribute(dt) is the ColBERT document tensor field and query(qt) is the ColBERT query tensor representation. The query(qt) tensor is defined in the passage schema:
query(qt) tensor>float<(qt{},x[32])
We configure the MaxSim operator in a Vespa ranking profile,
where we use the dense bi-encoder model as our first-phase ranking function and use the ColBERT MaxSim as the second phase ranking expression.
We use re-ranking count of 1000 (per node),
this setting can also be controlled by a query time setting,
in case we want to explore different re-ranking depths.
The ranking profile is given below.
In this case, we also cast the bfloat16 tensor values
to float to enable HW accelerations in place for operations on float tensors.
rank-profile e5-colbert inherits e5 {
inputs {
query(qt) tensor<float>(qt{},x[128])
query(q) tensor<>float<(x[384])
}
function cos_sim() {
expression: cos(distance(field, e5))
}
function max_sim() {
expression {
sum(
reduce(
sum(
query(qt) * unpack_bits(attribute(colbert)), x
),
max, dt
),
qt
)
}
}
second-phase {
rerank-count: 100
expression: max_sim()
}
match-features: max_sim() cos_sim()
}
Vespa ColBERT query encoder
We have trained a ColBERT model using a 6-layer MiniLM model, which can be downloaded from Huggingface model hub. This model only have 22.7M trainable parameters. This model can be served with Vespa using ONNX format.
ColBERT Ranking Evaluation
We evaluate the ranking effectiveness of the ColBERT model deployed as a re-ranking step on top of the dense retriever introduced in the previous post. We use MS Marco Passage Ranking dev query split (6980 queries):
| Retrieval method | Ranking | MRR@10 | Recall@100 | Recall@200 | Recall@1000 |
|---|---|---|---|---|---|
| weakAnd (sparse) | bm25 | 0.185 | 0.66 | 0.73 | 0.85 |
| nearestNeighbor (dense) | innerproduct | 0.310 | 0.82 | 0.87 | 0.94 |
| nearestNeighbor (dense) | ColBERT | 0.359 | 0.86 | 0.90 | 0.94 |
The Recall@1000 does not change as the model is used to re-rank the top 1K hits from the dense retriever. The Recall@100 and Recall@200 metrics improve with the ColBERT re-ranking step and MRR@10 improves from 0.310 to 0.359.
The end-to-end latency, including query encoding of the dense retriever model, ColBERT query encoding, retrieval with nearest neighbor search (with targetHits=1000) and re-ranking with ColBERT is just 39 ms. Reducing the nearest neighbor search targetHits, and also the re-ranking depth of the ColBERT model can be used to trade accuracy versus cost.
$ ./src/main/python/evaluate_passage_run.py --rank_profile dense-colbert --rerank_hits 1000 --retriever dense --ann_hits 1000 --hits 10 --trec_format --run_file dev.test --query_split dev --endpoint https://$ENDPOINT:4443/search/ 100%|█████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████████| 6980/6980 [04:27<00:00, 26.07it/s]
Summary
In this blog post we have demonstrated how to represent the ColBERT model as a re-ranking phase over a dense retriever using Vespa core capabilities:
- Dense retrieval accelerated by ANN query operator in Vespa (HNSW) and representing the Transformer based query encoder model(s) in Vespa
- Tensor fields in the document for fast access during re-ranking
- Express the MaxSim ColBERT late interaction similarity function using tensor ranking expressions
- Representing the ColBERT query encoder using ONNX format
In the fourth post in this series we will introduce another re-ranking step using a cross-encoder with all-to-all interaction. This cross-encoder model is also based on a small 6-layer MiniLM transformer model. We will deploy this model on top of the ColBERT re-ranking step, adding a third re-ranking step to further improve the ranking precision.